알고리즘/그래프의 기타 주제
[MST] Kruskal 알고리즘
- -
이번 포스트에서는 MST를 구하기 위한 Kruskal 알고리즘에 대해 살펴보자.
Kruskal 알고리즘
알고리즘 개요
크루스칼 알고리즘은 간선을 중심으로 MST를 구하는 알고리즘이다. 어차피 MST는 트리이므로 Circle을 만들지 않으면서 비용이 작은 간선들을 계속해서 연결하다보면 MST가 구성되는 특징을 이용한다.
Kruskal의 기본 동작은 다음과 같다.
- 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 연결해간다. - 이 과정에서 Circle이 발생하면 그 간선은 버리고 다음 간선을 선택한다.
- 트리이므로 N-1개의 간선이 선택되면 종료한다.
알고리즘 전개 절차
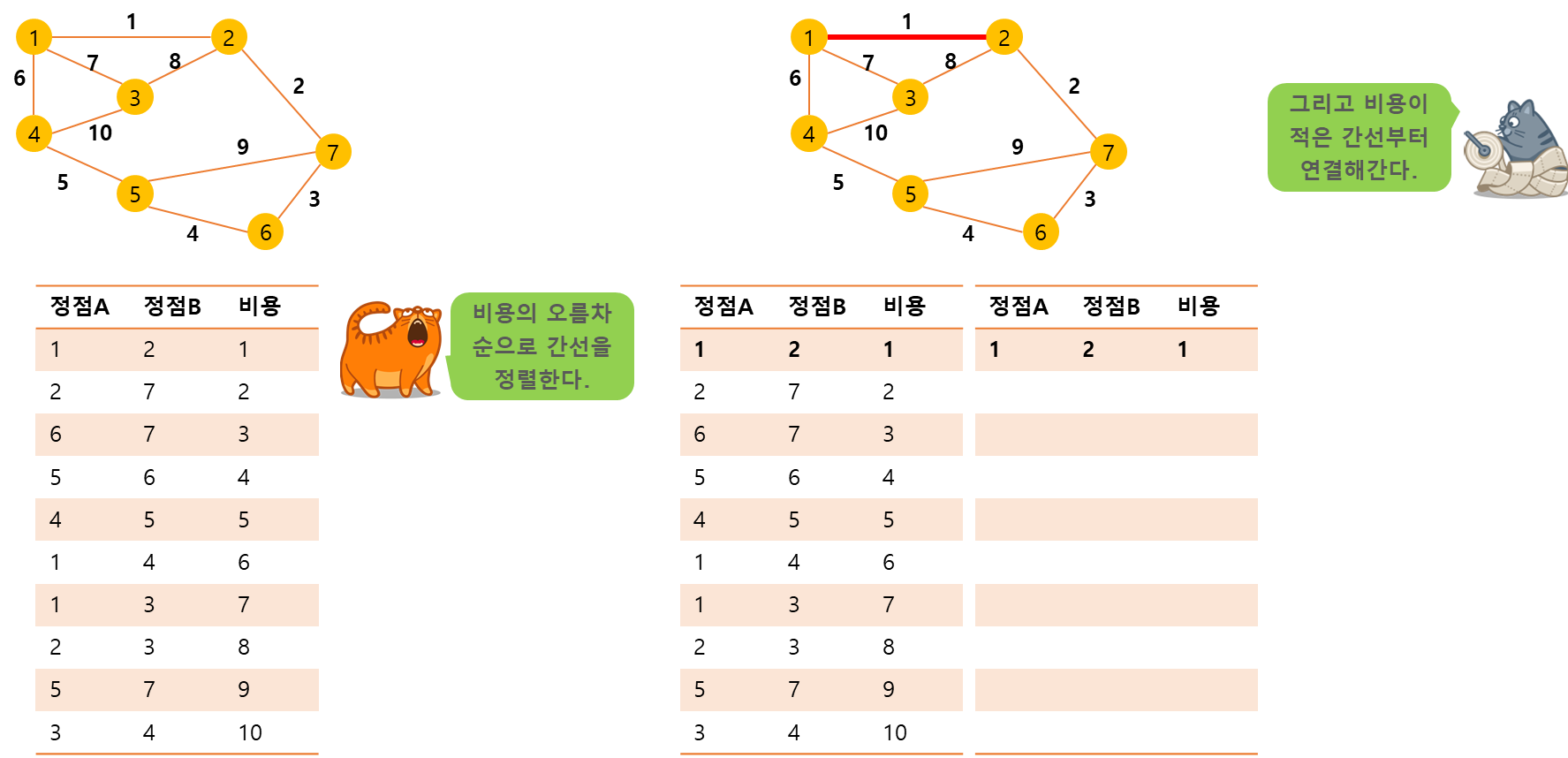

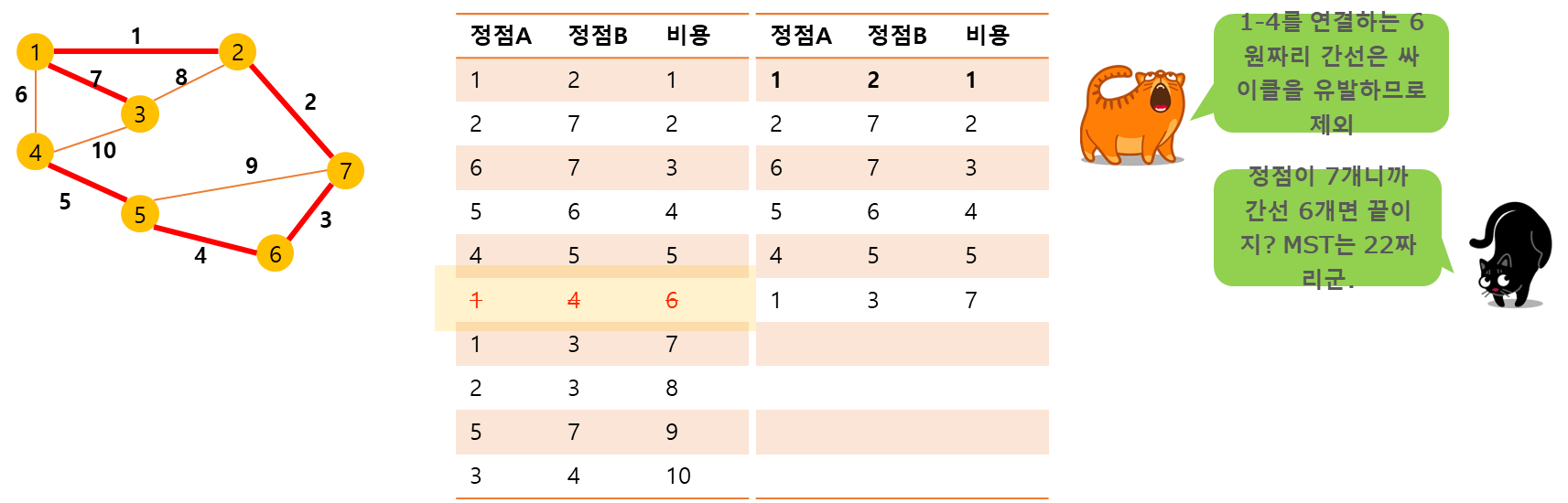
기본 코드
Kruskal은 최소 비용의 간선들을 연결하는 과정에서 Circle을 판별하기 위해 Union-Find 자료구조를 사용한다. 따라서 Union-Find 자료 구조만 잘 이해한다면 전혀 어려울게 없다.
일단 간선을 준비하는데 이것은 비용의 오름차순으로 정렬되어야 한다.
static class Edge implements Comparable<Edge> { // 간선 중심의 알고리즘
int a, b, w;
public Edge(int a, int b, int w) {
this.a = a;
this.b = b;
this.w = w;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.w, o.w); // 간선의 오름차순으로 정렬
}
}Union-Find를 이용해서 최소 비용의 간선을 N-1개 연결할 때까지 union 시킨다.
Edge[] edges = new Edge[E];
// 간선들을 정렬한다.
Arrays.sort(edges);
// union find 준비
makeSet();
// mst 간선의 개수는 V-1개
for (int i = 0; i < edges.length && mstCnt < V; i++) {
Edge edge = edges[i];
if (union(edge.a, edge.b)) { // 싸이클이 발생하지 않으면 연결
mstCnt++;
totalW += edge.w;
}
}
BJ 6497 전력난 솔루션(Kruskal)
package bj.gold.l4;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StringReader;
import java.util.Arrays;
import java.util.StringTokenizer;
/**
* @author 은서파
* @since 2020. 10. 12.
* @see https://www.acmicpc.net/problem/6497
* @git
* @youtube
* @performance 239752 752
* @category #크루스칼, #MST
* @note 모든 집은 서로 연결되어있다 - 완전 그래프
* 최소 비용으로 모두 연결 - MST
*/
public class BJ_G4_06497_전력난 {
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder output = new StringBuilder();
static StringTokenizer tokens;
static int N, M;
static Edge[] edges;
static long total;
static UnionFind uf;
public static void main(String[] args) throws IOException {
input = new BufferedReader(new StringReader(src));
while (true) {
// 변수 초기화 주의
total = 0;
tokens = new StringTokenizer(input.readLine());
M = Integer.parseInt(tokens.nextToken()); // 집의 수
N = Integer.parseInt(tokens.nextToken()); // 길의 수
if (M == 0 && N == 0) {
break;
}
edges = new Edge[N];
for (int n = 0; n < N; n++) {
tokens = new StringTokenizer(input.readLine());
int x = Integer.parseInt(tokens.nextToken());
int y = Integer.parseInt(tokens.nextToken());
int z = Integer.parseInt(tokens.nextToken());
total += z;
edges[n] = new Edge(x, y, z);
}
// 쿠르스칼은 간선을 정렬 후 사용
Arrays.sort(edges);
uf = new UnionFind(M);// 0 index
output.append(total - kruskal()).append("\n");
}
System.out.println(output);
}
static long kruskal() {
long mstCost = 0;
int mstCnt = 0;
for (int i = 0; i < edges.length; i++) {
Edge edge = edges[i];
if (uf.union(edge.from, edge.to)) {
mstCost += edge.cost;
// 최대 연결은 M-1개까지만
if (++mstCnt == M - 1) {
break;
}
}
}
return mstCost;
}
static class UnionFind {
int[] repres;
public UnionFind(int size) {
// makeSet()
repres = new int[size];
// 0 index
for (int i = 0; i < repres.length; i++) {
repres[i] = -1;
}
}
public int find(int x) {
if (repres[x] < 0) {
return x;
}
return repres[x] = find(repres[x]);
}
public boolean union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) {
return false;
} else {
repres[a] += repres[b];
repres[b] = a;
return true;
}
}
}
static class Edge implements Comparable<Edge> {
int from;
int to;
int cost;
public Edge(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
@Override
public String toString() {
return "Edge [from=" + from + ", to=" + to + ", cost=" + cost + "]";
}
@Override
// 적은 간선이 먼저 나오도록 처리
public int compareTo(Edge o) {
return Integer.compare(this.cost, o.cost);
}
}
// REMOVE_START
private static String src = "7 11\r\n" +
"0 1 7\r\n" +
"0 3 5\r\n" +
"1 2 8\r\n" +
"1 3 9\r\n" +
"1 4 7\r\n" +
"2 4 5\r\n" +
"3 4 15\r\n" +
"3 5 6\r\n" +
"4 5 8\r\n" +
"4 6 9\r\n" +
"5 6 11\r\n" +
"0 0";
// REMOVE_END
}
'알고리즘 > 그래프의 기타 주제' 카테고리의 다른 글
| [위상정렬] 1. 알고리즘 이해 (0) | 2024.11.22 |
|---|---|
| [서로소 집합] 개요 (0) | 2021.12.04 |
| [MST] Prim (0) | 2021.11.23 |
| [MST] 개요 (0) | 2020.06.06 |
Contents
소중한 공감 감사합니다