[위상정렬] 1. 알고리즘 이해
- -
이번 포스트에서는 위상정렬 알고리즘에 대해 살펴보자.
위상정렬 알고리즘
문제제시
https://www.acmicpc.net/problem/14567
위상정렬 알고리즘이란?
위상정렬(位相整列: Topological Sorting)이란 노드 간의 위치(선-후관계)에 따라 모든 정점들을 배열하는 작업을 말한다. 주로 업무의 일정을 일이 진행되어야 할 순서에 따라 배치하기 위해 사용되는 알고리즘이다.
대표적으로 과목들간의 선수관계에 따른 수강 계획을 작성한다든가 게임에서 어떤 빌딩을 생성하기 위한 테크트리를 떠올리면 쉽다.

대부분의 위상 정렬 문제들은 선-후 관계에 위배되지 않는 경우 중 하나를 출력하는 문제들이다.
그래프 요소들이 정렬되기 위해서는 당연히 명확한 순서가 있어야 한다. 따라서 위상 정렬은 DAG(directed acyclic graph: 유향의 비순환 그래프)에서만 의미가 있다.
즉 닭이 먼저인지, 달걀이 먼저인지 처럼 선행 요소를 알 수 없는 경우는 사용할 수 없다.
위상정렬은 크게 다음과 같이 3단계를 거친다.
- 자기 자신을 가리키는 간선이 없는 정점(꼭지점, 진입 차수가 0인 지점)들을 찾는다. 이 정점들의 이전 정점은 없으므로 이 꼭지점들은 탐색의 기점이 된다. 만약 이런 정점이 없으면 종료된다.
- 1에서 찾은 정점을 출력하고 이 정점에서 출발한 간선들을 제거한다. 결과로 도착점의 진입 차수들이 1씩 감소하게 된다.
- 다시 1부터 반복한다.
위 과정을 수행하기 위해서는 아래와 같이 2개의 준비물이 필요하다.
- 각 정점 별로 몇 개의 간선이 자신을 가리키는지 관리하기 위한 배열: int [] indegrees
- 꼭지점들을 관리하기 위한 Queue, List 등의 자료 구조
알고리즘 수행 과정
아래와 같이 구성된 그래프가 있을 때 가능한 위상정렬의 예를 구해보자. 아래의 그래프에서 1, 4, 6의 선-후 관계는 알 수 없다.
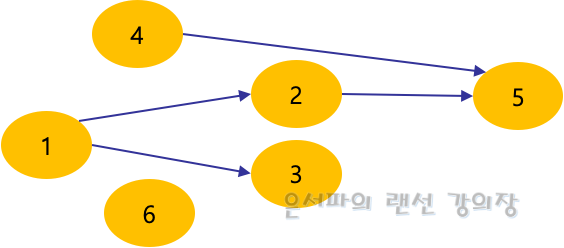
먼저 그래프들의 진입 차수를 계산해보면 다음과 같다.
| 정점번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 진입차수 | 0 | 1 | 1 | 0 | 2 | 0 |
이 지점들 중 진입 차수가 0인 1, 4, 6번은 이전 정점이 없기 때문에 바로 처리될 수 있는 정점들로 탐색의 출발점이 된다. 이 정점들을 List, Queue 등의 자료구조를 이용해서 저장해보자. 전술했듯이 1, 4, 6의 순서는 무의미하다.

이제 Queue에서 하나씩 빼면서 값을 출력하고 각 정점에서 시작된 간선들을 하나씩 지워가며 진입차수 테이블을 갱신한다. 이 행위가 바로 선행 작업이 끝났음을 의미한다. 위 상황에서는 1-> 2, 1-> 3, 4->5번 간선이 삭제될 것이다.
출력의 예는 [1, 4, 6]된다.

수행 결과 진입차수 테이블은 아래이 변경된다.
| 정점번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 진입차수 | 0 | 0 | 0 | 0 | 1 | 0 |
이제 새롭게 진입차수가 0이 된 지점들은 선수 정점들의 처리가 다 끝났다는 의미이므로 현 시점의 제일 선행 정점이 된다. 다시 이 정점들을 Queue에 넣어보자.

역시 하나씩 출력하며 연결된 간선을 제거해보면 다음의 결과를 얻게 된다.
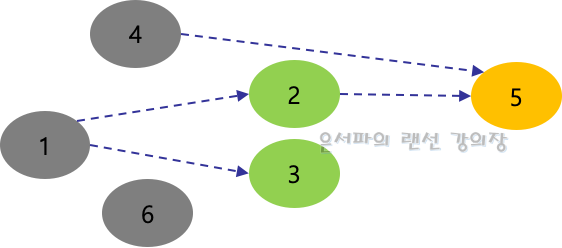
출력 결과는 [1, 4, 6, 2, 3]이고 진입차수 테이블은 아래와 같이 변경된다.
| 정점번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 |
다시 새롭게 진입차수가 0이된 5를 Queue에 넣고 동일한 과정을 거치면 이제 모든 정점에 대한 탐색이 종료된다.
최종적인 출력 결과 중 하나는 [1, 4, 6, 2, 3, 5]가 된다. 이 값은 선후 관계를 위반하지 않은 예 중의 하나가 된다. 물론 4,1,6,3,2,5도 답이 될 수 있기 때문에 많은 문제에서는 "정렬된 순서로 방문하라"와 같은 조건이 붙기도 한다.
기본 코드 및 시간 복잡도
package basecode.graph;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StringReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;
/**
* @author 은서파
* @since 2022. 8. 29.
*/
public class TopologySorting {
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder output = new StringBuilder();
static StringTokenizer tokens;
static int V, E;
static LinkNode[] graph;
static int[] indegrees;
public static void main(String[] args) throws IOException {
input = new BufferedReader(new StringReader(src));
tokens = new StringTokenizer(input.readLine());
V = Integer.parseInt(tokens.nextToken());
E = Integer.parseInt(tokens.nextToken());
graph = new LinkNode[V + 1];
indegrees = new int[V + 1];
for (int e = 0; e < E; e++) {
tokens = new StringTokenizer(input.readLine());
int a = Integer.parseInt(tokens.nextToken());
int b = Integer.parseInt(tokens.nextToken());
//위상정렬은 directed acyclic graph에서만 가능
graph[a] = new LinkNode(b, graph[a]);
indegrees[b]++;
}
topologySort(indegrees);
}
static void topologySort(int[] indegrees) {
Queue<Integer> q = new ArrayDeque<>();
// 모든 정점들을 대상으로 초기 탐색 -O(V)
for(int v=1; v<indegrees.length; v++) {
// 진입차수가 0인 정점들이 초기 탐색 시점
if(indegrees[v]==0) {
q.offer(v);
}
}
// 결국은 모든 정점들을 대상으로 연결된 간선들 탐색 - O(E)
while(!q.isEmpty()) {
Integer head = q.poll();
output.append(head).append(' ');
// 그래프 탐색
for(LinkNode next = graph[head]; next!=null; next = next.next) {
indegrees[next.i]--;
if(indegrees[next.i]==0) {
q.offer(next.i);
}
}
}
System.out.println(output);
}
static class LinkNode {
int i;
LinkNode next;
public LinkNode(int i, LinkNode next) {
this.i = i;
this.next = next;
}
}
// REMOVE_START
private static String src = "6 4\n" // 정점 개수, 간선 개
+ "1 2\n" // 간선 정보
+ "1 3\n"
+ "2 5\n"
+ "4 5";
// REMOVE_END
}위의 코드에서 topologySort()를 살펴보면 모든 정점들의 진입 차수를 계산하는데 O(V), 정점을 통해 모든 간선을 탐색하는데 O(E)의 시간이 소요되서 전체적으로 O(V+E)의 시간 복잡도를 갖는 것을 알수 있다.
사이클의 판단
앞서 위상정렬이 성공하려면 반드시 DAG(directed acyclic graph: 유향 비순환 그래프)여야 한다고 했는데 이를 거꾸로 이야기 하면 위상정렬이 실패한다면 순환 그래프라는 말이 된다.
다음의 간단한 순환 그래프를 살펴보자.

이 그래프의 진입 차수를 계산해보면 아래와 같다.
| 정점번호 | 1 | 2 | 3 |
| 진입차수 | 0 | 2 | 1 |
따라서 1번 정점을 Queue에 넣을꺼고

빼면서 진입차수를 갱신해보면 아래의 결과를 얻는다.
| 정점번호 | 1 | 2 | 3 |
| 진입차수 | 0 | 1 | 1 |
이제 진입차수가 0인 정점이 없으므로 Queue는 비어있게 된다. 탐색이 종료되지만 2번과 3번 정점은 서로가 간선을 교환하고 있기 때문에 위상정렬은 실패하게 되고 사이클이 발생했음을 알 수 있다.
// 사이클 체크: 진입차수가 0이 아닌 정점이 있는지 확인
for(int v = 1; v < indegrees.length; v++) {
if(indegrees[v] > 0) return false; // 사이클 존재
}
주요 키워드
- 순서 관련 키워드
- "선수 과목", "선행 조건", "선후 관계", "순서가 정해져있는", "먼저 해야하는", "의존성", "prerequisite"
- 방향성 관련 키워드
- "A가 B보다 앞서야 한다", "A 다음에 B가 온다", "A를 완료해야 B를 시작할 수 있다", "A -> B"
- 작업/과정 관련 키워드
- "작업 순서", "공정", "단계", "과정", "진행 순서", "건설 순서", "조립 순서",
- 시간/스케줄 관련 키워드
- "최소 몇 학기가 필요한지", "가장 빠른 시간", "완료하는데 걸리는 시간", "스케줄링"
'알고리즘 > 그래프의 기타 주제' 카테고리의 다른 글
| [서로소 집합] 개요 (0) | 2021.12.04 |
|---|---|
| [MST] Prim (0) | 2021.11.23 |
| [MST] Kruskal 알고리즘 (0) | 2021.11.16 |
| [MST] 개요 (1) | 2020.06.06 |
소중한 공감 감사합니다