투포인터
- -
이번에 살펴볼 투 포인터나 다음에 살펴볼 슬라이딩 윈도우는 모두 1차원 배열 상에서 O(N*M)의 시간 복잡도로 해결해야 할 일들을 O(N)에 해결하게 도와주는 알고리즘이다.
특별하게 코드가 복잡하지도 않고 쉽게 이해할 수 있는데 왕왕 써먹을데가 많은 알고리즘 중 하나이다.
투 포인터(Two Pointer) 알고리즘
문제 살펴보기
먼저 Tow Pointer를 이용해서 풀어볼 수 있는 간단한 문제를 살펴보자.
https://www.acmicpc.net/problem/2018
2018번: 수들의 합 5
어떠한 자연수 N은, 몇 개의 연속된 자연수의 합으로 나타낼 수 있다. 당신은 어떤 자연수 N(1 ≤ N ≤ 10,000,000)에 대해서, 이 N을 몇 개의 연속된 자연수의 합으로 나타내는 가지수를 알고 싶어한
www.acmicpc.net
기본적인 접근
주어진 숫자를 구성할 수 있는 연속된 자연수의 구성을 찾아야 하는 문제이다. 여기서 중요한 키워드는 연속된 자연수 이다.
만약 15가 주어졌다면 이를 만들수 있는 구성은 아래와 같이 4가지 이다.
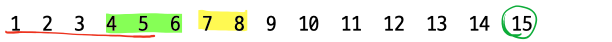
어떻게 찾아보면 좋을까? brute force 적으로 접근해보자.
1부터 쭉 더해가다보면 1+2+3+4+5에서 15가 구성되서 탐색이 종료된다. 그럼 1을 출발점으로 하는 구성은 완료이다.
다음은? 당연히 2부터 더해가야 한다. 2+3+4+5=14니까 6까지 더해야 하는데 이제 20이 되어서 15를 한참 넘는다. 따라서 2에서 시작하는 것은 답이 없다.
다음은 3부터, 그리고 4부터 이런식으로 N개의 숫자에 대해 N개까지는 아니지만 연속된 M개의 수를 쭉 더해가는 과정이 필요하다. 따라서 시간 복잡도는 O(N*M)이 된다.
문제는 N 제한이 1 ≦N≦10,000,000 이므로 M이 100만 되어도 100억번의 연산이 필요해서 시간 초과가 발생한다.
투포인터의 컨셉
투 포인터 알고리즘의 컨셉은 안된다고해서 버려지는 것을 정말 버리지 말고 잘 활용해보는데 있다. 그리고 그 전제 조건으로는 데이터의 연속성이 필요하다.
이 문제에서는 "몇 개의 연속된 자연수의 합으로 나타낼 수 있는가?" 를 물어보고 있으므로 데이터의 연속성이 확보된 상태이다.
만약 2(si=1)에서 탐색을 시작해서 값을 누적시킨다고 생각해보자. 값을 계속 누적시키다가 6(ei=5)인 지점에 오면 누적 합이 20이 되어서 탐색은 실패한다.

여기서 중요한 사실은 지금까지 더해온 2+3+4+5+6이 틀렸다고 해서 버려버리면 안된다는 점이다.
20을 좀 줄여가볼 수는 없을까? 이 숫자들은 오름 차순으로 연속되어있기 때문에 ei가 증가하면 수는 계속 증가해버린다. 하지만 si를 증가시키면? 2+3+4+5+6에서 3+4+5+6이 되므로 18로 줄어들게 된다.
중요한 점은 3+4+5+6은 이미 계산한 적이 있기때문에 새롭게 계산하지 않고 지난 계산에서 2만 빼주면 된다.!! 여기서 연산의 회수가 반복구조 O(M)에서 O(1)로 떨어지게 된다.
물론 여전히 15를 만족하지는 못한다.값을 더 줄여야 하기 때문에 si를 한칸 더 전진 시켜보자. 그럼 4+5+6이 되어서 총 합은 15가 나온다. 성공!
이제 답이 되는 경우를 하나 찾았으니 다시 si를 전진시켜보자. 이제는 5+6이어서 11이다. 15가 되기 위해서는 보다 큰 수가 필요하다. 따라서 ei를 증가시켜 5+6+7을 만들어본다.
18로 너무 크면 다시 si를 증가시켜서 6+7을 만들고 너무 작으니까 6+7+8, 다시 너무 크니까 7+8로 만들어 다시 15를 만드는데 성공한다.
이런 식으로 탐색하다 보면 인덱스가 변경될 때 O(1)의 상수시간 연산만 추가되기 때문에 결국 O(N)의 시간 복잡도에 문제를 해결할 수 있게 된다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StringReader;
import java.util.StringTokenizer;
/**
* @author 은서파
* @since 2022. 7. 9.
* @see https://www.acmicpc.net/problem/2018
* @git https://github.com/quietjun/algo_aps/blob/master/src/bj/silver/l5/BJ_S5_02018_%EC%88%98%EB%93%A4%EC%9D%98%ED%95%A95.java
* @youtube
* @performance 11572 104
* @category #투포인터
* @note
*/
public class BJ_S5_02018_수들의합5 {
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder output = new StringBuilder();
static StringTokenizer tokens;
static int N;
static int CNT = 1; // 최초 자기 스스로가 하나
public static void main(String[] args) throws IOException {
input = new BufferedReader(new StringReader(src));
N = Integer.parseInt(input.readLine());
if(N==1) {
System.out.println(CNT);
return;
}
int sum = 1;
for(int si=1, ei=1; si<=N/2;) { // si가 절반 이상으로 갈 경우는 없다.
if(sum < N) {
// ei를 증가해서 더해주기
sum+=++ei;
}else if(sum >N) {
// si를 빼고 증가하기
sum-=si++;
}else {
CNT++;
// 현재의 si를 빼고 si는 증가
sum-=si++;
}
}
System.out.println(CNT);
}
// REMOVE_START
private static String src = "15";
// REMOVE_END
}
또다른 형태의 전개
투 포인터는 크게 2가지 형태로 진행된다.
- 두 개의 포인터가 같은 방향으로 진행하기(fast pointer, last pointer)
- 하나의 포인터는 왼쪽 끝-> 오른쪽, 다른 하나는 오른쪽 끝 -> 왼쪽으로 진행하기(left pointer, right pointer)
그냥 방향이 다를 뿐 기본적인 개념과 전개 방식은 동일하다.
첫 번째 문제의 형태를 앞서 살펴본 형태이고 두 번째 형태의 문제를 살펴보자.
문제 살펴보기
https://www.acmicpc.net/problem/1940
1940번: 주몽
첫째 줄에는 재료의 개수 N(1 ≤ N ≤ 15,000)이 주어진다. 그리고 두 번째 줄에는 갑옷을 만드는데 필요한 수 M(1 ≤ M ≤ 10,000,000) 주어진다. 그리고 마지막으로 셋째 줄에는 N개의 재료들이 가진 고
www.acmicpc.net
기본적인 접근
이 문제는 각각의 재료들이 고유한 번호를 가지고 있고 여기서 두개씩 재료를 합해서 M의 범위에 드는 구성의 개수를 찾아줘야 한다.
예를 들어 재료가 2, 7, 4, 1, 5, 3으로 주어졌다면 아래와 같이 전개가 가능하다.

이 경우 시간 복잡도는 O(N*N)인데 문제의 N제한이 15000이므로 상당히 버겁다.( 연산 회수는 약 2억2천으로 간신히 통과 하긴 한다.)
투포인터 활용
이 문제는 두 수를 더해서 값이 일정 값이 유지되는 경우를 찾아주면 된다. 즉 어떤 수를 가지고 값이 크면 줄여주고 작으면 늘여주면 된다. 다행히 주어진 숫자를 오름 차순으로 정렬해서 나열하면 왼쪽에서 오른쪽으로 갈 때는 증가하고 오른쪽에서 왼쪽으로 갈 때에는 수가 줄어든다.
따라서 맨 왼쪽(li)과 오른쪽 끝(ri)에서 두 개의 포인터를 출발시켜서 값을 더해보고 값이 너무 크면 줄여야 하니까 ri를 1줄여서 다시 계산해보고 값이 너무 작으면 키워야 하니까 li를 1늘여서 다시 계산해주면 된다.
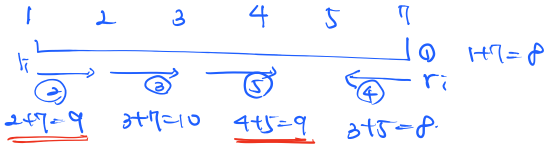
package bj.silver.l4;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StringReader;
import java.util.Arrays;
import java.util.StringTokenizer;
/**
* @author 은서파
* @since 2022. 7. 10.
* @see https://www.acmicpc.net/problem/1940
* @git https://github.com/quietjun/algo_aps/blob/master/src/bj/silver/l4/BJ_S4_01940_주몽.java
* @youtube
* @performance 투포인터: 15100 148, 단순: 15092 260
* @category #투포인터
* @note
*/
public class BJ_S4_01940_주몽 {
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder output = new StringBuilder();
static StringTokenizer tokens;
static int N;
static int M;
static int [] NUMS;
static int ANS;
public static void main(String[] args) throws IOException {
input = new BufferedReader(new StringReader(src));
N = Integer.parseInt(input.readLine());
M = Integer.parseInt(input.readLine());
NUMS = new int[N];
tokens = new StringTokenizer(input.readLine());
for(int i=0; i<N; i++) {
NUMS[i] = Integer.parseInt(tokens.nextToken());
}
//simple();
twoPointer();
}
private static void twoPointer() {
Arrays.sort(NUMS);
ANS = 0;
for(int l=0, r=N-1, sum=0; l<r; ) {
sum = NUMS[l]+NUMS[r] ;
if(sum==M) {
ANS++;
l++;
r--;
}else if(sum<M) {
l++;
}else {
r--;
}
}
System.out.println(ANS);
}
private static void simple() {
ANS = 0;
for(int n1=0; n1<N; n1++ ) {
for(int n2 = n1+1; n2<N; n2++ ) {
if(NUMS[n1]+NUMS[n2]==M) {
//System.out.println(n1+" : "+n2);
ANS++;
}
}
}
System.out.println(ANS);
}
// REMOVE_START
private static String src = "6\n"
+ "9\n"
+ "2 7 4 1 5 3";
// REMOVE_END
}
'알고리즘 > 기타' 카테고리의 다른 글
| APS에 유용한 chrome plugin (1) | 2024.11.27 |
|---|---|
| 슬라이딩 윈도우 알고리즘 (0) | 2024.11.26 |
| [python]string에서 입력 받기 (0) | 2022.05.28 |
| APS를 시작하기 전에 읽어두면 좋을 내용들 (0) | 2021.02.25 |
소중한 공감 감사합니다